Functional form

Functional form

Further information: Molecular mechanics

Molecular mechanics potential energy function with continuum solvent.

The basic functional form of a force field encapsulates both bonded terms relating to atoms that are linked by covalent bonds, and nonbonded (also called "noncovalent") terms describing the long-range electrostatic and van der Waals forces. The specific decomposition of the terms depends on the force field, but a general form for the total energy in an additive force field can be written as where the components of the covalent and noncovalent contributions are given by the following summations: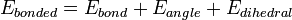


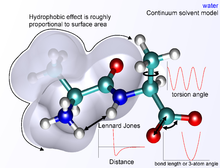
The bond and angle terms are usually modeled as harmonic oscillators in force fields that do not allow bond breaking. A more realistic description of a covalent bond at higher stretching is provided by the more expensive Morse potential. The functional form for the rest of the bonded terms is highly variable. Proper dihedral potentials are usually included. Additionally, "improper torsional" terms may be added to enforce the planarity of aromatic rings and other conjugated systems, and "cross-terms" that describe coupling of different internal variables, such as angles and bond lengths. Some force fields also include explicit terms for hydrogen bonds.
The nonbonded terms are most computationally intensive because they include many more interactions per atom. A popular choice is to limit interactions to pairwise energies. The van der Waals term is usually computed with a Lennard-Jones potential and the electrostatic term with Coulomb's law, although both can be buffered or scaled by a constant factor to account for electronic polarizability and produce better agreement with experimental observations.